Archív značky pro: bílý šum

Tvoříme si vlastní trh… v Excelu

V tomto příspěvku vám dám návod, jak si během pár minut snadno v Excelu vytvoříte vlastní „trh“ a lépe tak pochopíte, jak se tržní cena vlastně chová. Současně si prakticky ověříte informace, které podávám v tomto dvoudílném pojednání o technické analýze a v tomto vysvětlení náhodné procházky a bílého šumu.

Prvním krokem je logicky zapnout Excel. Než s ním ale začnete pracovat, budete jej potřebovat rozšířit o add-on nazvaný Analýza dat. To uděláte v sekci Možnosti, tlačítko do ní se nachází na výchozí obrazovce úplně vlevo dole. Pokud pracujete s nějakým dokumentem, do výchozí obrazovky se dostanete tlačítkem Soubor.

V možnostech vyberte v levém menu Doplňky (druhé odspoda). Při tomto kroku se mi Excel často na pár vteřit sekne, vydržte tedy, než se mu podaří zmátořit. Poté už byste měli vidět seznam doplňků a hned první vás zajímá – Analytické nástroje. Zvolte jej a klikněte na tlačítko Přejít… Zde zaškrtněte první volbu – Analytické nástroje (nebo i další položky dle libosti, třeba řešitel je také užitečný nástroj). Potvrďte OK a mělo by být hotovo. Pro kontrolu po otevření nějakého sešitu běžte do sekce Data a zde by úplně vlevo měla být nová ikona Analýza dat.

Všechno potřebné pro tvorbu grafu připomínajícího ten tržní nyní máte. V souladu s definicemi je potřeba nejprve vygenerovat bílý šum. Vstupte nyní do nové sekce ve vašem Excelu – Analýza dat.

V seznamu analytických nástrojů vyberte Generátor pseudonáhodných čísel a zvolte OK. Nyní je potřeba nastavit vlastnosti souboru pseudonáhodných čísel tak, aby odpovídaly vlastnostem bílého šumu.

  • Počet proměnných je počet vygenerovaných souborů hodnot. Jedna proměnná = jeden bílý šum = jedna náhodná procházka = jeden graf.
  • Počet náhodných čísel je velikost souboru. Doporučuji alespoň několik stovek.
  • Typ rozložení: Normální. To je velice důležité.
  • Střední hodnota = 0. Pokud se rozhodnete experimentovat a zvolíte kladné číslo, bude vám výsledná náhodná procházka trendovat vzhůru, pokud zvolíte záporné číslo, bude trendovat dolů.
  • Směrodatná odchylka = 1. Pokud se rozhodnete experimentovat, zvyšováním hodnoty zvýšíte volatilitu procházky a naopak.
  • Základ generátoru můžeme nechat prázdný.
  • V možnostech výstupu vyberte, kam se mají hodnoty vašeho bílého šumu vložit

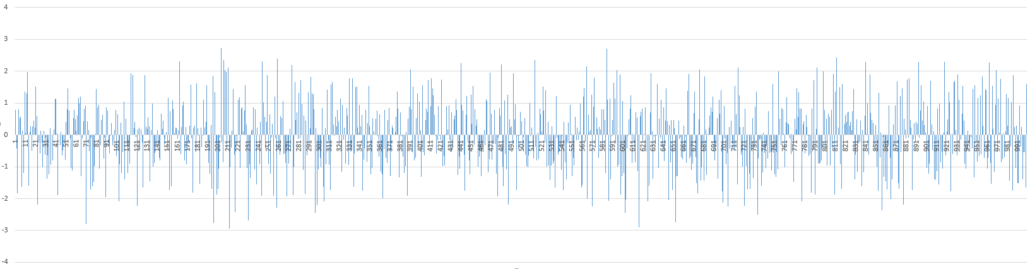
Měli byste obdržet sloupec plný různých desetinných čísel. Pokud jste je zadali stejně jako na obrázku a soubor převedete do grafu, měli byste spatřit něco podobného:


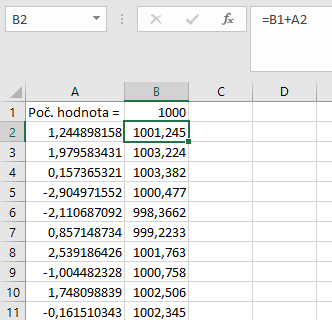
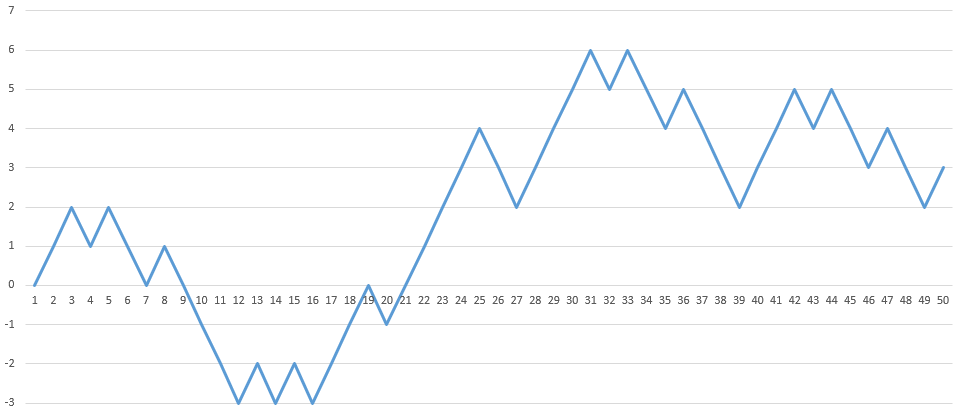
Jde o grafické znázornění bílého šumu. Teď už jen tuto změť převést na náhodnou procházku. Bude to snadné. Vraťte se ke sloupci vygenerovaného bílého šumu (na obrázku sloupec A) a vložte nad hodnoty jeden prázdný řádek (označte první řádek kliknutím na jedničku nalevo od buněk, klikněte pravým tlačítkem a zvolte Vložit buňky). Ideálně ve vedlejším sloupci B teď vytvoříme náhodnou procházku. V buňce B1 se nachází pole pro určení počáteční hodnoty. Obvykle se nechává 0, ale my můžeme zvolit třeba 1000, aby výsledek věrněji připomínal vývoj ceny tržního instrumentu, v tomto případě třeba zlata nebo akcií Googlu. Do pole B2 vepíšeme vzorec =B1+A2, tedy každá další hodnota bude součtem aktuální hodnoty a nové hodnoty bílého šumu, přesně jak tomu má být. Pak už jen dvakrát poklepeme na čtvereček vpravo dole obdélníku označené buňky a sloupec B se sám dopočítá až do konce podle sloupce A. Sloupec B převeďte na graf a máte hotovo. U mě výsledek vypadá takto:

Váš graf by měl vypadat jinak, protože vám Excel vygeneroval jiný soubor pseudonáhodných čísel, stejně tak by měl dopadnout jinak každý další pokus. Vždy by měl výsledek ale vypadat přibližně jako burzovní graf. Hraní si s počátečními hodnotami, směrodatnými odchylkami, středními hodnotami a dalšími proměnnými můžu jedině doporučit, lépe tak pochopíte, o co zde vlastně jde. Také si všimněte, že na každý takto vygenerovaný graf můžete aplikovat technickou analýzu. To by vás mělo zarazit. Rozepisuji se o tom v tomto dvoučlánku.

Náhodná procházka aneb chůze opilce

V tomto článku se nebudu zabývat mou opileckou procházkou po okolí Liberce, nýbrž půjde o pravděpodobnostní pojem důležitý pro porozumění vývoji tržních cen finančních instrumentů. Pokusím se jej vysvětlit tak, aby jej pochopil i lajk. Náhodná procházka má uplatnění v mnoha různých vědních oborech, já se jí budu zabývat samozřejmě z hlediska oboru studujícího časové řady, neboť mezi časové řady patří právě i vývoj ceny jakéhokoliv finančního instrumentu.

50 kroků opilce

Náhodné procházce se také někdy přezdívá chůze opilce. Uznejme, že chůze opilce mnohdy náhodná skutečně je. Je to takový proces, jehož přírůstky mají náhodný směr. Stejně jako opilec jde jednou doprava, jindy doleva. V tom, kde skončí jeho další krok, nelze vypozorovat žádný systém, nemůžeme tedy směřování jeho dalšího kroku určit předem. Je to podobné, jako kdyby o směru každého dalšího kroku rozhodl hod mince. Pana = doleva, orel = doprava, například. Pokud uvážíme, že každý krok je stejně dlouhý, může po padesáti krocích taková procházka při pohledu shora vypadat třeba takto:


Náhodná procházka s 50 kroky při stejné velikosti kroku.

Pokud bychom našeho opilce znovu postavili na startovní čáru, je zřejmé, že dalších 50 kroků by vypadalo jinak, ale výsledná cestička by měla podobnou chaotickou strukturu. Nelze třeba čekat, že by šel všech 50 kroků jen doleva, i když to nemožné není. Procházky můžeme posléze hodnotit podle jejich vlastností. Ta na obrázku se například dostala nejdále 3 kroky doprava a 6 kroků doleva, dále bychom mohli vypočítat směrodatnou odchylku a další ukazatele, ale o tom už tento článek není. Abychom se dostali, kam potřebujeme, budeme teď potřebovat ještě jednu úpravu. Vyzkoušíme náhodnou procházku, ve které není délka kroku pevně stanovena. Podobně, jako kdyby se opilec ve svém stavu občas posunul třeba jen o třicet centimetrů a jindy zavrávoral a skončil by třeba o 3 metry jinde. Přírůstky teď budou mít nejenom náhodný směr, ale i náhodnou vzdálenost. Vzdálenost bude náhodná, ale přesto ohraničená. Je jasné, že se opilec jedním krokem neposune o 100 metrů.

Představujeme: bílý šum

Když si teď vezmeme ony přírůstky jako soubor hodnot (tedy třeba 1 metr, 50 cm, 80 cm apod.), můžeme určit nějaké vlastnosti tohoto souboru. Je potřeba určit velikost běžného kroku, což by mohlo být kolem 70 cm. To je jakýsi průměrný krok, který nastane s nejvyšší pravděpodobností, v řeči statistiky střední hodnota. Čím kratší nebo delší krok než těch 70 cm, tím nižší pravděpodobnost, že nastane. Pak je ještě potřeba stanovit průměrnou odchylku od oněch 70 cm. Statisticky to je směrodatná odchylka a v tomto případě dejme tomu 20 cm. No a na závěr pravděpodobnostní rozdělení. Tím vás nechci trápit, vezmeme normální (gaussovské) rozdělení, což zjednodušeně znamená to, co jsem už napsal – nejvíce kroků se bude koncentrovat v okolí 70 cm a čím dále, tím méně. Teď konečně přijde rozuzlení toho, proč se tu bavíme o vlastnostech přírůstků. Pro modelování vývoje cen se totiž používá náhodná procházka generovaná přírůstky s vlastnostmi takzvaného bílého šumu.

Bílý šum je takový soubor hodnot, jehož střední hodnota = 0, směrodatná odchylka = 1 a má normální (gaussovské) rozdělení. Trochu lidověji řečeno to znamená, že tyto hodnoty se budou motat kolem 0 a jejich průměrná vzdálenost od nuly bude 1. Průměr budou značně zvyšovat ojedinělé výrazně vzdálené hodnoty, třeba 2,5 apod. Čím dále, tím méně pravděpodobné je, že se tam číslo objeví. Příklad bílého šumu s 1000 členy je třeba na tomto obrázku. Můžete si od oka všimnout, že uvedené vlastnosti skutečně splňuje.

Bílý šum s 1000 členy, střední hodnotou 0 a směrodatnou odchylkou 1.
Praktický návod: vytvořte si také vlastní trh v Excelu

Konečně: náhodná procházka

Teď se vraťme k náhodné procházce. Vytvořme tedy takovou náhodnou procházku, jejíž přírůstky budou mít vlastnosti bílého šumu. Startovní číslo dáme 0 a přičítáme jednotlivé hodnoty náhodně vygenerovaného bílého šumu. Vznikne něco podobného jako tento graf:


Náhodná procházka s přírůstky o vlastnostech bílého šumu.

Povědomé, že? Pokud bych startovní bod dal třeba do 12000, mohl bych vám klidně namluvit, že jde o graf německého akciového indexu DAX. Dokonce lze na první pohled rozeznat malé i velké trendy, supporty a rezistence, zkrátka vlastnosti, které v trzích rozeznáváme. O tom ale více v tomto dvoučlánku.

Náhodná procházka má samozřejmě spousty různých podob, tato má nejblíže ke struktuře trhů. Snadno můžeme vytvořit trendující náhodnou procházku, můžeme si hrát s vlastnostmi bílého šumu a tedy s velikostmi přírůstků. Pokud si chcete tvořit vlastní trhy v Excelu a vše, co jsem napsal, si ověřit, je to velice snadné. Návod naleznete v tomto článku.