Náhodná procházka aneb chůze opilce
V tomto článku se nebudu zabývat mou opileckou procházkou po okolí Liberce, nýbrž půjde o pravděpodobnostní pojem důležitý pro porozumění vývoji tržních cen finančních instrumentů. Pokusím se jej vysvětlit tak, aby jej pochopil i lajk. Náhodná procházka má uplatnění v mnoha různých vědních oborech, já se jí budu zabývat samozřejmě z hlediska oboru studujícího časové řady, neboť mezi časové řady patří právě i vývoj ceny jakéhokoliv finančního instrumentu.
50 kroků opilce
Náhodné procházce se také někdy přezdívá chůze opilce. Uznejme, že chůze opilce mnohdy náhodná skutečně je. Je to takový proces, jehož přírůstky mají náhodný směr. Stejně jako opilec jde jednou doprava, jindy doleva. V tom, kde skončí jeho další krok, nelze vypozorovat žádný systém, nemůžeme tedy směřování jeho dalšího kroku určit předem. Je to podobné, jako kdyby o směru každého dalšího kroku rozhodl hod mince. Pana = doleva, orel = doprava, například. Pokud uvážíme, že každý krok je stejně dlouhý, může po padesáti krocích taková procházka při pohledu shora vypadat třeba takto:
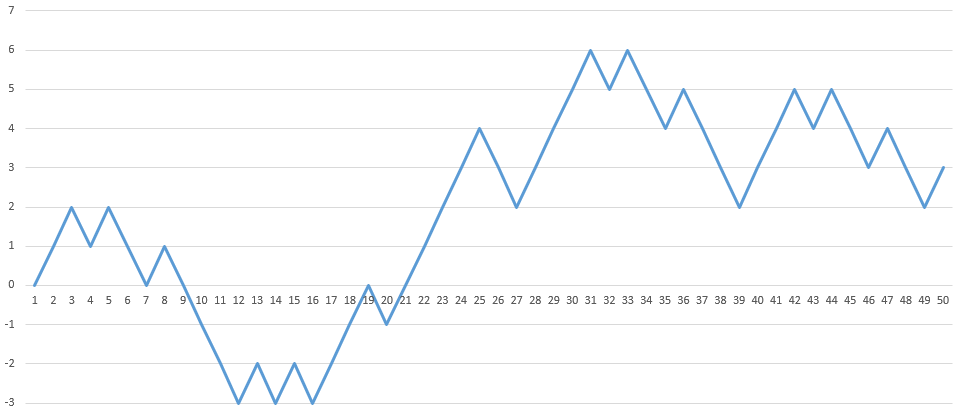
Náhodná procházka s 50 kroky při stejné velikosti kroku.
Pokud bychom našeho opilce znovu postavili na startovní čáru, je zřejmé, že dalších 50 kroků by vypadalo jinak, ale výsledná cestička by měla podobnou chaotickou strukturu. Nelze třeba čekat, že by šel všech 50 kroků jen doleva, i když to nemožné není. Procházky můžeme posléze hodnotit podle jejich vlastností. Ta na obrázku se například dostala nejdále 3 kroky doprava a 6 kroků doleva, dále bychom mohli vypočítat směrodatnou odchylku a další ukazatele, ale o tom už tento článek není. Abychom se dostali, kam potřebujeme, budeme teď potřebovat ještě jednu úpravu. Vyzkoušíme náhodnou procházku, ve které není délka kroku pevně stanovena. Podobně, jako kdyby se opilec ve svém stavu občas posunul třeba jen o třicet centimetrů a jindy zavrávoral a skončil by třeba o 3 metry jinde. Přírůstky teď budou mít nejenom náhodný směr, ale i náhodnou vzdálenost. Vzdálenost bude náhodná, ale přesto ohraničená. Je jasné, že se opilec jedním krokem neposune o 100 metrů.
Představujeme: bílý šum
Když si teď vezmeme ony přírůstky jako soubor hodnot (tedy třeba 1 metr, 50 cm, 80 cm apod.), můžeme určit nějaké vlastnosti tohoto souboru. Je potřeba určit velikost běžného kroku, což by mohlo být kolem 70 cm. To je jakýsi průměrný krok, který nastane s nejvyšší pravděpodobností, v řeči statistiky střední hodnota. Čím kratší nebo delší krok než těch 70 cm, tím nižší pravděpodobnost, že nastane. Pak je ještě potřeba stanovit průměrnou odchylku od oněch 70 cm. Statisticky to je směrodatná odchylka a v tomto případě dejme tomu 20 cm. No a na závěr pravděpodobnostní rozdělení. Tím vás nechci trápit, vezmeme normální (gaussovské) rozdělení, což zjednodušeně znamená to, co jsem už napsal – nejvíce kroků se bude koncentrovat v okolí 70 cm a čím dále, tím méně. Teď konečně přijde rozuzlení toho, proč se tu bavíme o vlastnostech přírůstků. Pro modelování vývoje cen se totiž používá náhodná procházka generovaná přírůstky s vlastnostmi takzvaného bílého šumu.
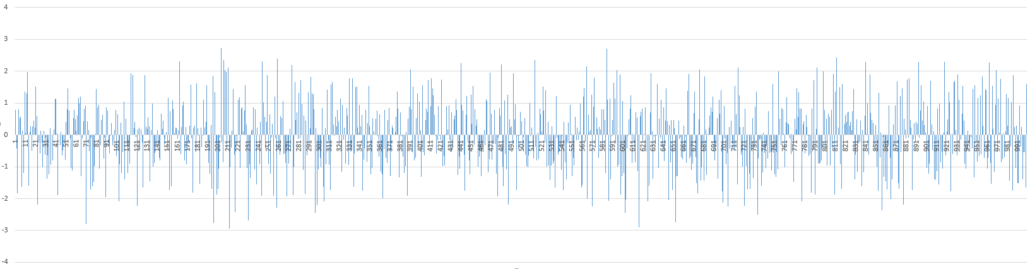
Bílý šum je takový soubor hodnot, jehož střední hodnota = 0, směrodatná odchylka = 1 a má normální (gaussovské) rozdělení. Trochu lidověji řečeno to znamená, že tyto hodnoty se budou motat kolem 0 a jejich průměrná vzdálenost od nuly bude 1. Průměr budou značně zvyšovat ojedinělé výrazně vzdálené hodnoty, třeba 2,5 apod. Čím dále, tím méně pravděpodobné je, že se tam číslo objeví. Příklad bílého šumu s 1000 členy je třeba na tomto obrázku. Můžete si od oka všimnout, že uvedené vlastnosti skutečně splňuje.
Konečně: náhodná procházka
Teď se vraťme k náhodné procházce. Vytvořme tedy takovou náhodnou procházku, jejíž přírůstky budou mít vlastnosti bílého šumu. Startovní číslo dáme 0 a přičítáme jednotlivé hodnoty náhodně vygenerovaného bílého šumu. Vznikne něco podobného jako tento graf:
Povědomé, že? Pokud bych startovní bod dal třeba do 12000, mohl bych vám klidně namluvit, že jde o graf německého akciového indexu DAX. Dokonce lze na první pohled rozeznat malé i velké trendy, supporty a rezistence, zkrátka vlastnosti, které v trzích rozeznáváme. O tom ale více v tomto dvoučlánku.
Náhodná procházka má samozřejmě spousty různých podob, tato má nejblíže ke struktuře trhů. Snadno můžeme vytvořit trendující náhodnou procházku, můžeme si hrát s vlastnostmi bílého šumu a tedy s velikostmi přírůstků. Pokud si chcete tvořit vlastní trhy v Excelu a vše, co jsem napsal, si ověřit, je to velice snadné. Návod naleznete v tomto článku.




Leave a Reply
Want to join the discussion?Feel free to contribute!